All about R

SIMPLE Variable assignment and use of FUNCTIONS
 a<-4 nbsp="" p="">a/2=2
a*2=8
b<-1 nbsp="" p="">a+b=5, a-b=3, b-a=-3
sin(a), cos(b)
a==b False or F
a>b TRUE or T

VECTOR
Null in SQL= NA in R
sum(a, na.rm=True) will add all values without NA
x<-c p="">names(x)<-c asters="" br="" college="" school="">
plot(x)
y<-1:4 p="">print(y) 1,2,3,4

MATRIX
create matrix
matrix(1,3,4) corresponds to matric(value in each column, rows, columns)
A<-matrix p="">contour(A) -----creates a graph for matrix so its easily readable

3D prespective plot:
persp(a)

3D perspective with less expansion
persp(a,expand=0.2)

R includes some sample data sets to play around with. One of these is volcano, a 3D map of a dormant New Zealand volcano.

contour(volcano)
persp(volcano, expand=0.2)
image(volcano) ------image function create a heat map 

SUMMARY STATISTICS
http://www.ltcconline.net/greenl/courses/201/descstat/mean.htm

• Average value (mean)=sum(n)/n
• Most frequently occurring value (mode)
• On average, how much each measurement deviates from the mean Formula
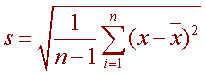  Variance and Standard Deviation: Step by Step 
  Calculate the mean, x.  
  Write a table that subtracts the mean from each observed value.
  Square each of the differences.
  Add this column. 
  Divide by n -1 where n is the number of items in the sample  This is the variance.
  To get the standard deviation we take the square root of the variance.  

 finally, Mean+sd and mean-sd is the range in which the values should lie, other are outliers.

• Span of values over which your data set occurs (range), and
• Median= average of two middle values when ordered asc or desc in series (this value gives a better and robust idea of an average than mean, since it does not take outliers in consideration)

mean(volcano)
barplot(x)
> limbs<-c br="">> mean(limbs) 3.428571
> names(limbs)<-c br="" five="" four="" one="" seven="" six="" three="" two="">> barplot(limbs)
> abline(h=mean(limbs)) --horizon
median(limbs) = 4
sd(limbs) =0.7867958
abline(h=mean(limbs)+sd(limbs),lty"dotted",col="red")
abline(h=mean(limbs)+sd(limbs))

Factors

Data Frames

type<-c gems="" gold="" p="" silver="">weight<-c p="">prices<-c br="">

> treasure <- code="" data.frame="" prices="" types="" weights=""> 

> print(treasure) 

    weights prices  types
1     300   9000   gold
2     200   5000 silver
3     100  12000   gems
4     250   7500   gold
5     150  18000   gems

treasure[[2]]= treasure[["prices"]] = treasure$prices

[1]  9000  5000 12000  7500 18000 

Read files

read.csv("C:\\Program Files\\R\\targets.csv") 

read.table("C:\\Program Files\\R\\Infantry.txt",sep="\t")

read.table("C:\\Program Files\\R\\Infantry.txt",sep="\t",header=TRUE)

 plot(countries$GDP,countries$Piracy)

 cor.test(countries$GDP, countries$Piracy)
Pearson's product-moment correlation

data:  countries$GDP and countries$Piracy 
t = -14.8371, df = 107, p-value < 2.2e-16

Conventionally, any correlation with a p-value less than 0.05 is 
considered statistically significant, and this sample data's p-value is 
definitely below that threshold. In other words, yes, these data do show
 a statistically significant negative correlation between GDP and 
software piracy.   

 If we know a country's GDP, can we use that to estimate its piracy rate?

We can, if we calculate the linear model that best represents all our data points (with a certain degree of error). The lm function takes a model formula, which is represented by a response variable (piracy rate), a tilde character (~), and a predictor variable (GDP). (Note that the response variable comes first.)
Try calculating the linear model for piracy rate by GDP, and assign it to the line variable:

 line <- b="" countries="" iracy="" lm="">

Other statistical packages that can be added to R

install.packages("ggplot2")